Theoretische Grundlagen

Gegeben sei eine ebene homogene Platte (das Grundgebiet), an deren Rand ein Temperaturprofil vorgegeben ist (Abb.

). Entsprechend diesem Profil wird sich auf der Platte eine bestimmte Temperaturverteilung einstellen.

**Abbildung:** Geometrie des Dirichlet-Problems.
$\includegraphics[width=0.7\textwidth]{temp1.eps}$

u(x, y) sei die Temperatur auf der Platte im Punkt (x, y). Wenn es im Inneren des Grundgebietes keine Wärmequellen gibt, gehorcht die Temperaturverteilung der homogenen partiellen Differentialgleichung

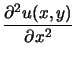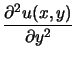$\displaystyle {\frac{{\partial ^{2} u(x,y)}}{{\partial x^{2}}}}$$ + $\displaystyle {\frac{{\partial ^{2} u(x,y)}}{{\partial y^{2}}}}$$ = 0 .

(1)

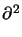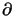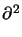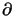Der Differential-Operator $\partial^{{2}}_{}$$ / $\partial$$ x² + $\partial^{{2}}_{}$$ / $\partial$$ y² ist der zweidimensionale Laplace-Operator, und die elliptische Differentialgleichung (

) heißt dementsprechend die zweidimensionale Laplace-Gleichung.

Das der Platte aufgeprägte Temperaturprofil wird durch die Randbedingung

u(x, y)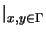 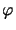$\displaystyle \mid_{{x,y \in \Gamma}}^{}$$ = $\displaystyle \varphi$$ (x, y)

(2)

beschrieben, wobei 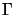$\Gamma$$ die Randkurve des Grundgebietes bedeutet.

Die Gleichungen () und () definieren eine inhomogene, partielle Randwertaufgabe zweiter Ordnung. Auf Grund der Form der gegebenen Randbedingung spricht man von einem Dirichletschen Problem.

Christian Sommer 2002-01-21