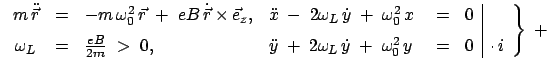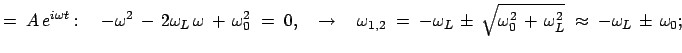Unterabschnitte
Die Newtonsche Bewegungsgleichung (3.1) gilt nur in Inertialsystemen. Untersucht
man einen Bewegungsvorgang in einem System, das kein Inertialsystem ist,
dann muß man Zusatzeffekte berücksichtigen, die von der beschleunigten Bewegung
des Systems und der Trägheit der Massen herrühren. In den Bewegungsgleichungen
treten dann neben den eingeprägten Kräften noch die Trägheitskräfte auf.
Inertialsysteme
Ein System heißt Inertialsystem, wenn in ihm ein Körper keine Beschleunigung
erfährt, wenn keine äußeren Kräfte auf ihn wirken:
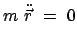 wenn wenn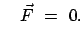 |
(81) |
Wir betrachten die Menge der Inertialsysteme. Das erste sei das von Gl. (8.1).
Ein zweites sei:
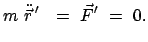 |
(82) |
Aus (8.1) und (8.2) folgt, daß die Beschleunigungen gleich sein müssen.
Zweimalige Integration dieser Gleichung gibt:
Die letzte Beziehung besagt, daß es eine 6-parametrige Menge von Inertialsystemen
gibt. Jedes Element ist durch ein spezielles Wertesextupel der Integrationskonstanten
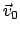 und
und 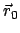 gekennzeichnet. Die Erfahrung zeigt, daß es
solche Koordinatensysteme tatsächlich gibt: Systeme, die relativ zum Fixsternhimmel
in gleichförmiger Bewegung sind, sind in guter Näherung Inertialsysteme.
gekennzeichnet. Die Erfahrung zeigt, daß es
solche Koordinatensysteme tatsächlich gibt: Systeme, die relativ zum Fixsternhimmel
in gleichförmiger Bewegung sind, sind in guter Näherung Inertialsysteme.
Wir betrachten zwei rechtshändige Koordinatensysteme (Abb. 8.1). Das erste
System,  , mit den orthonormierten Basisvektoren
, mit den orthonormierten Basisvektoren
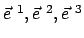 heißt raumfestes System; es ist ein Inertialsystem. Das zweite System,
heißt raumfestes System; es ist ein Inertialsystem. Das zweite System,  ,
ist ebenfalls ein rechtshändiges mit den orthonormierten Basisvektoren
,
ist ebenfalls ein rechtshändiges mit den orthonormierten Basisvektoren
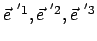 ; es heißt körperfestes System.
Es wird später ein bewegtes, sogar beschleunigtes System
sein; zunächst wird es ebenfalls als fix betrachtet. Der Vektor
; es heißt körperfestes System.
Es wird später ein bewegtes, sogar beschleunigtes System
sein; zunächst wird es ebenfalls als fix betrachtet. Der Vektor 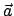 weist vom
Ursprung
weist vom
Ursprung 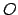 des Systems
des Systems 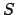 zum Ursprung
zum Ursprung 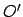 von
von  . Zu ein- und demselben Raumpunkt
. Zu ein- und demselben Raumpunkt
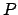 weist von
weist von 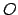 der Vektor
der Vektor 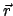 (mit Komponenten
(mit Komponenten 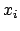 bezüglich
bezüglich 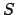 )
und von
)
und von 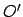 der Vektor
der Vektor
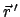 (mit Komponenten
(mit Komponenten 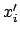 bezüglich
bezüglich  ) :
) :
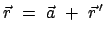 |
(84) |
In 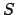 lauten die Komponenten dieser Vektorgleichung:
lauten die Komponenten dieser Vektorgleichung:
Die
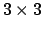 Matrix
Matrix
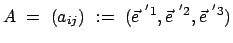 mit mit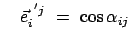 |
(86) |
ist aus den Komponenten gebildet, die die Basisvektoren
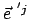 des Systems
des Systems  bezüglich
bezüglich 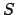 haben; sie werden durch Normalprojektion der Einheitsvektoren
haben; sie werden durch Normalprojektion der Einheitsvektoren
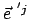 auf die Koordinatenachsen von
auf die Koordinatenachsen von 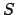 gebildet und sind gleich den
Richtungskosinussen, Abb. 8.2(a). Der Winkel
gebildet und sind gleich den
Richtungskosinussen, Abb. 8.2(a). Der Winkel
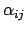 liegt in der Ebene, die von den
beiden eben genannten Vektoren aufgespannt wird. Die Drehmatrix
liegt in der Ebene, die von den
beiden eben genannten Vektoren aufgespannt wird. Die Drehmatrix
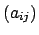 ist reell
und orthogonal:
ist reell
und orthogonal:
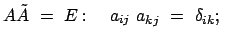 (a) (a)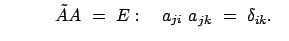 (b) (b) |
(87) |
Für den Spezialfall, daß die Ursprünge der beiden Systeme zusammenfallen und
das gestrichene System  gegenüber dem ungestrichenen
gegenüber dem ungestrichenen 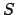 um den Winkel
um den Winkel 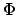 verdreht
ist, ergibt sich (Abb. 8.2(b)):
verdreht
ist, ergibt sich (Abb. 8.2(b)):
![$\displaystyle A = \left( \begin{array}{ccc} \cos \Phi & - \sin \Phi & 0 [1mm] \sin \Phi & \cos \Phi & 0 [1mm] 0 & 0 & 1 \end{array} \right) .$](img1636.gif) |
(88) |
Echte Vektoren können parallel zu sich selbst im Raum
verschoben werden. Sie lassen sich als Differenzen von Ortsvektoren darstellen.
Gemäß dieser Definition ergibt sich aus (8.5)
für echte Vektoren das folgende Transformationsgesetz
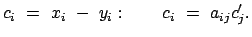 |
(89) |
Die Eulerschen Winkel
Abbildung 8.3:
Die Eulerschen Winkel.
|
![\includegraphics[scale=0.8]{k8_eulerwinkel}](img1638.gif) |
Wenn zwei rechtshändige Koordinatensystem irgendwie zueinander stehen, kann man das eine in das
andere durch zwei Operationen überführen: 1) durch eine Translation um einen Vektor  schiebt man den einen Ursprung in den anderen; 2) durch eine Drehung bringt man entsprechende
Koordinatenachsen zur Deckung. Diese Drehung kann auf mehrere Weisen festgelegt werden. Hier
werden nur zwei behandelt: a) die Angabe eines Drehvektors: b) durch drei Winkel, die
Eulerschen Winkel.
schiebt man den einen Ursprung in den anderen; 2) durch eine Drehung bringt man entsprechende
Koordinatenachsen zur Deckung. Diese Drehung kann auf mehrere Weisen festgelegt werden. Hier
werden nur zwei behandelt: a) die Angabe eines Drehvektors: b) durch drei Winkel, die
Eulerschen Winkel.
Wir beschränken uns nun auf die Drehungen, setzen also bis auf weiteres den Vektor  in Gl. (8.5) Null.
Eine Drehung kann durch die Angabe eines Einheitsvektors
in Gl. (8.5) Null.
Eine Drehung kann durch die Angabe eines Einheitsvektors 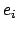 für die Drehachse und
eines Drehwinkels
für die Drehachse und
eines Drehwinkels 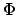 festgelegt werden. Dann kann man die Komponenten der Basisvektoren
des gedrehten Systems
festgelegt werden. Dann kann man die Komponenten der Basisvektoren
des gedrehten Systems 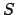 mittels des Drehtensors berechnen:
mittels des Drehtensors berechnen:
Diese Darstellung hat den Nachteil, daß
die 4 Parameter
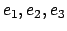 und
und 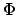 einer Nebenbedingung unterworfen sind (
einer Nebenbedingung unterworfen sind (
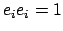 ).
).
Es ist zweckmäßiger, ein System von 3 Winkeln zu verwenden, die voneinander unabhängig sind. Ein
solches sind eben die Eulerschen Winkel. Diese geben die Lage des körperfesten
Systems  relativ zu raumfesten
relativ zu raumfesten 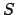 an. Letzteres wird in seine in Abb. 8.3
angegebene Endlage in 3 Schritten übergeführt:
Zuerst wird das gestrichene System um die 3-Achse (die 3'-Achse fällt während dieses
Schrittes noch mit der 3-Achse zusammen) um den Winkel
an. Letzteres wird in seine in Abb. 8.3
angegebene Endlage in 3 Schritten übergeführt:
Zuerst wird das gestrichene System um die 3-Achse (die 3'-Achse fällt während dieses
Schrittes noch mit der 3-Achse zusammen) um den Winkel 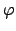 in positivem Sinn gedreht.
Die neue Lage der 1'-Achse heißt die Knotenlinie.
Im zweiten Schritt wird das körperfeste System um die Knotenlinie um
den Winkel
in positivem Sinn gedreht.
Die neue Lage der 1'-Achse heißt die Knotenlinie.
Im zweiten Schritt wird das körperfeste System um die Knotenlinie um
den Winkel 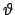 gedreht. Diesen Winkel schließen auch die 1'-, 2'-Ebene
und die 1-, 2-Ebene ein. Die momentane Stellung der 2'-Achse gibt die
Querachse. Im letzten Schritt werden die 1'- und 2'-Achse um den Winkel
gedreht. Diesen Winkel schließen auch die 1'-, 2'-Ebene
und die 1-, 2-Ebene ein. Die momentane Stellung der 2'-Achse gibt die
Querachse. Im letzten Schritt werden die 1'- und 2'-Achse um den Winkel
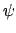 um die 3'-Achse in die Endlage gedreht.
um die 3'-Achse in die Endlage gedreht.
Der vom gemeinsamen Ursprung 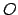 beider Systeme zum Punkt
beider Systeme zum Punkt 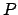 weisende Vektor
weisende Vektor 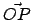 hat in
hat in 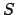 die Komponenten
die Komponenten 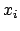 , in
, in  die Komponenten
die Komponenten 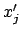 .
.
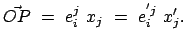 |
(812) |
Die Komponenten werden gemäß Gl. (8.5) umgerechnet:
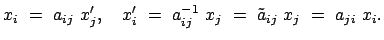 |
(813) |
Die orthogonale Transformationsmatrix ist gegeben durch:
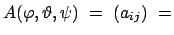 |
(814) |
Diese Matrix kann berechnet werden, indem man zuerst die einzelnen Drehungen ausrechnet.
Diese sind
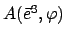 ,
,
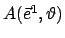 und
und
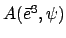 .
Die erste und die letzte Drehmatrix ergeben sich aus (8.8), indem man für
.
Die erste und die letzte Drehmatrix ergeben sich aus (8.8), indem man für 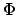 den entsprechenden Winkel einsetzt. Für die Drehung um die Knotenlinie findet man:
Die gesamte Drehmatrix ergibt sich dann durch Matrizenmultiplikation und liefert obige
Matrix (8.14).
den entsprechenden Winkel einsetzt. Für die Drehung um die Knotenlinie findet man:
Die gesamte Drehmatrix ergibt sich dann durch Matrizenmultiplikation und liefert obige
Matrix (8.14).
Für ein anderes Verfahren wird Gl. (8.12) mit 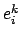 überschoben, der resultierende
Ausdruck wird mit Gl. (8.5) verglichen. Dies gibt:
überschoben, der resultierende
Ausdruck wird mit Gl. (8.5) verglichen. Dies gibt:
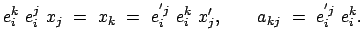 |
(815) |
Die Matrixelemente 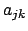 können also aus den inneren Produkten der
Basisvektoren bestimmt werden. Die Basisvektoren von
können also aus den inneren Produkten der
Basisvektoren bestimmt werden. Die Basisvektoren von 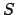 sind einfach,
Gl. (8.16a); die Komponenten der Basisvektoren
sind einfach,
Gl. (8.16a); die Komponenten der Basisvektoren
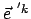 in
in 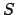 berechnet man mit
Hilfe der Abb. 8.3.
berechnet man mit
Hilfe der Abb. 8.3.
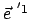 und
und
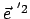 kann man zunächst auf
kann man zunächst auf
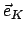 (in Richtung der Knotenlinie) und
(in Richtung der Knotenlinie) und 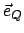 (in Richtung der Querachse)
aufspannen. Wir geben die benötigten Basisvektoren an, bei manchen werden für spätere
Anwendungen die Komponenten bezüglich
(in Richtung der Querachse)
aufspannen. Wir geben die benötigten Basisvektoren an, bei manchen werden für spätere
Anwendungen die Komponenten bezüglich  und
und  benötigt.
benötigt.
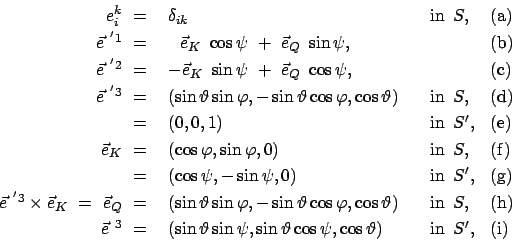 |
(816) |
Jetzt nehmen wir an, die Lage des körperfesten Systems  ändert sich im
Laufe der Zeit. In
der Transformationsgleichung (8.5) sind der Vektor
ändert sich im
Laufe der Zeit. In
der Transformationsgleichung (8.5) sind der Vektor
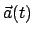 und die Matrixelemente
und die Matrixelemente
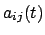 Funktionen der Zeit. Dies muß bei der Berechnung der Geschwindigkeit
Funktionen der Zeit. Dies muß bei der Berechnung der Geschwindigkeit
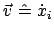 und der Beschleunigung
und der Beschleunigung
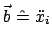 berücksichtigt werden.
berücksichtigt werden.
Hiebei ist eine gesonderte Untersuchung der Zeitableitung einer
orthogonalen Transformationsmatrix nötig. In diesem Fall unterscheiden sich die symbolische
und die analytische (Tensor-)schreibweise mehr als sonst. Deshalb geben wir diese Ableitung
in beiden Fällen an. Die symbolische Schreibweise erscheint einfacher und übersichtlicher,
bei der Berechnung komplifzierterer Probleme kann die analytische vorteilhafter sein.
Es gibt ja zwei Bezugssysteme, das raumfeste und das körperfeste. Jede symbolische Gleichung
muß bei einer konkreten Rechnung in einem der beiden Systeme ausgewertet werden und dies kann
in komplexeren Fällen schwierig werden. Bei der analytischen Schreibweise sind die Formeln
länglicher weil die Transformationen zwischen den Systemen immer explizit angegeben sind.
Die Drehung des körperfesten Systems kann durch einen Vektor beschrieben werden, der
die Winkelgeschwindigkeit genannt wird. Dies ist anschaulich klar. Wir zeigen jetzt wie
die zeitliche Änderung der Basisvektoren durch diesen Vektor ausgedrückt werden kann.
Die Basisvektoren
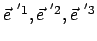 des rotierenden
Koordinatensystems sind normiert und stehen paarweise aufeinander orthogonal:
des rotierenden
Koordinatensystems sind normiert und stehen paarweise aufeinander orthogonal:
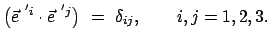 |
(817) |
Sie sind zeitabhängig. Die Zeitableitung steht auf dem ursprünglichen Vektor senkrecht,
wie aus Gl. (8.17) folgt.
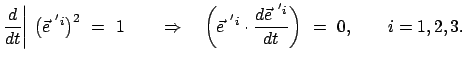 |
(818) |
Das Vektorprodukt zweier Basisvektoren gibt den dritten. Durch Differentiation nach der
Zeit folgt daraus:
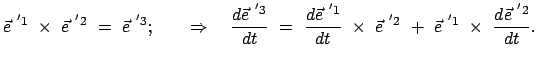 |
(819) |
Daraus folgt durch vektorielle Multiplikation mit
 :
:
Skalare Multiplikation der letzten Gleichung mit
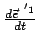 macht auch
den dritten Term zu Null. Gleichzeitig gibt dies das Spatprodukt:
macht auch
den dritten Term zu Null. Gleichzeitig gibt dies das Spatprodukt:
Differenziert man Gl. (8.17) für 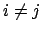 nach der Zeit, findet man:
nach der Zeit, findet man:
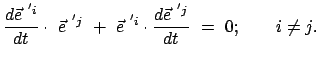 |
(820) |
Deswegen ist der zweite Faktor der vorletzten Gleichung Null, damit auch das Spatprodukt
der Zeitableitungen der Basisvektoren; diese liegen daher in einer Ebene.
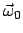 sei ein Einheitsvektor senkrecht zu dieser Ebene.
Wegen Gln. (8.18) und (8.20) steht
sei ein Einheitsvektor senkrecht zu dieser Ebene.
Wegen Gln. (8.18) und (8.20) steht
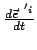 senkrecht auf
senkrecht auf
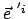 und auf
und auf
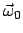 . Daher kann man die Zeitableitungen der
Basisvektoren schreiben als:
. Daher kann man die Zeitableitungen der
Basisvektoren schreiben als:
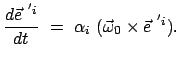 |
(821) |
In obiger Gleichung darf über den wiederholten Index 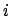 nicht summiert werden.
Setzt man (8.21) in (8.20) ein, ergeben sich:
und zwei analoge Gleichungen für
nicht summiert werden.
Setzt man (8.21) in (8.20) ein, ergeben sich:
und zwei analoge Gleichungen für
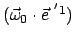 und
und
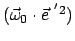 . Da die drei Basisvektoren paarweise
orthogonal sind, können nicht alle drei inneren Produkte
. Da die drei Basisvektoren paarweise
orthogonal sind, können nicht alle drei inneren Produkte
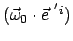 gleichzeitig Null sein. Daher müssen alle drei
Differenzen der
gleichzeitig Null sein. Daher müssen alle drei
Differenzen der 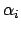 Null, also alle drei
Null, also alle drei 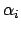 gleich sein. Damit kann man
Gl. (8.21) in folgender endgültiger Form schreiben:
gleich sein. Damit kann man
Gl. (8.21) in folgender endgültiger Form schreiben:
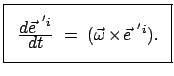 |
(822) |
Der Vektor
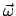 ist der Vektor der Winkelgeschwindigkeit, wie er auch unten
in Gl. (8.28) definiert ist. Seine Richtung gibt die Richtung der Drehachse, seine Länge
den Betrag der Winkelgeschwindigkeit an.
ist der Vektor der Winkelgeschwindigkeit, wie er auch unten
in Gl. (8.28) definiert ist. Seine Richtung gibt die Richtung der Drehachse, seine Länge
den Betrag der Winkelgeschwindigkeit an.
Bei der Berechnung der Geschwindigkeit durch Differentiation des Ortsvektors nach der
Zeit muß man beachten, daß auch die Basisvektoren des bewegten Systems Funktionen der
Zeit sind.
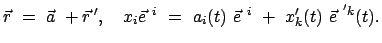 |
(823) |
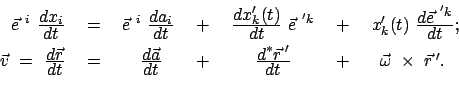 |
(824) |
Zur Umrechnung des letzten Termes der letzten Gleichung wurde
Gl. (8.21) herangezogen.
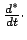 bedeutet, daß bei der Ableitung nur die gestrichenen Koordinaten nach der Zeit differenziert
werden, nicht aber die zeitabhängigen Basisvektoren. Die Geschwindigkeit im raumfesten
System wie diese auf der linken Seite steht, wird auf der rechten Seite aus drei Beiträgen
zusammengesetzt:
1) Aus der Bewegung des Ursprungs
bedeutet, daß bei der Ableitung nur die gestrichenen Koordinaten nach der Zeit differenziert
werden, nicht aber die zeitabhängigen Basisvektoren. Die Geschwindigkeit im raumfesten
System wie diese auf der linken Seite steht, wird auf der rechten Seite aus drei Beiträgen
zusammengesetzt:
1) Aus der Bewegung des Ursprungs  des gestrichenen Systems
des gestrichenen Systems  ,
2) aus der Geschwindigkeit des Massenpunktes relativ
,
2) aus der Geschwindigkeit des Massenpunktes relativ  und 3) aus der Drehung des Systems
und 3) aus der Drehung des Systems
 .
.
Wird Gl. (8.24) nach der Zeit differenziert, erhält man die Beschleunigung. Auf der rechten
Seite werden wieder die Zeitableitungen
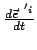 gemäß
Gl. (8.22) ersetzt.
Dies gibt dann:
gemäß
Gl. (8.22) ersetzt.
Dies gibt dann:
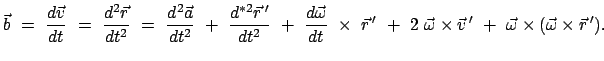 |
(825) |
Die Beschleunigung im raumfesten System kann zusammengesetzt werden aus:
1) der Beschleunigung des Urprungs  ,
,
2) der Relativbeschleunigung,
3) der Winkelbeschleunigung der Drehungs von  ,
,
4) der Coriolisbeschleunigung,
5) der Zentripetalbeschleunigung.
Die Newtonsche Bewegungsgleichung
gilt nur im raumfesten System, da dieses nach Voraussetzung ein Inertialsystem ist.
Aus der obigen Gleichung für die Beschleunigung
kann man aber eine Gleichung für die Beschleunigung relativ zu  bilden:
bilden:
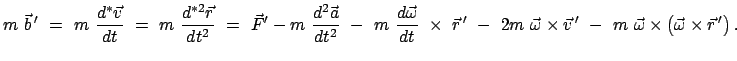 |
(826) |
Die Beschleunigung relativ zu  wird verursacht durch 1) die eingeprägte Kraft
wird verursacht durch 1) die eingeprägte Kraft 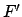 (der Strich bedeutet, daß die eingeprägte Kraft ins beschleunigte System umgerechnet
werden muß) und aus den Trägheitskräften 2) resultierend aus der beschleunigten
Bewegung von
(der Strich bedeutet, daß die eingeprägte Kraft ins beschleunigte System umgerechnet
werden muß) und aus den Trägheitskräften 2) resultierend aus der beschleunigten
Bewegung von 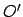 , 3) aus der beschleunigten Drehung von
, 3) aus der beschleunigten Drehung von  , 4) aus der Corioliskraft und
5) aus der Zentrifugalkraft.
, 4) aus der Corioliskraft und
5) aus der Zentrifugalkraft.
Wir gehen von Gl. (8.5) aus. Im allg. sind die Komponenten 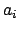 des
Translationsvektors
und die Elemente
des
Translationsvektors
und die Elemente 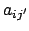 der Drehmatrix gegebene Funktionen der Zeit. Wieder ist eine
gesonderte Untersuchung der Zeitableitung dieser Matrix nötig; dies führt
neuerlich auf den
Vektor der Winkelgeschwindigkeit mit den Komponenten
der Drehmatrix gegebene Funktionen der Zeit. Wieder ist eine
gesonderte Untersuchung der Zeitableitung dieser Matrix nötig; dies führt
neuerlich auf den
Vektor der Winkelgeschwindigkeit mit den Komponenten 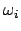 .
.
Wir betrachten zunächst eine reine Drehung, also Gl. (8.5) mit
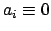 ; daher
ist
; daher
ist  . Ebenso sei der Punkt
. Ebenso sei der Punkt  fix in
fix in  (Abb. 8.3):
(Abb. 8.3):
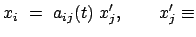 const. const. |
(827) |
Die Matrixelemente 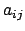 der Drehmatrix sind miteinander verknüpft durch die
Orthonormierungsrelationen (8.9). Von diesen wird das System (a) nach
der Zeit abgeleitet:
Man sieht: Die Matrix
der Drehmatrix sind miteinander verknüpft durch die
Orthonormierungsrelationen (8.9). Von diesen wird das System (a) nach
der Zeit abgeleitet:
Man sieht: Die Matrix
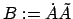 ist schiefsymmetrisch. Sie enthält (wie auch jeder
schiefsymmetrsiche Tensor 2. Stufe in 3 Dimensionen) nur drei unabhängige Elemente. Daher kann man
ist schiefsymmetrisch. Sie enthält (wie auch jeder
schiefsymmetrsiche Tensor 2. Stufe in 3 Dimensionen) nur drei unabhängige Elemente. Daher kann man
 einen dreidimensionalen Vektor zuordnen. Dafür wählen wir folgende Definition:
einen dreidimensionalen Vektor zuordnen. Dafür wählen wir folgende Definition:
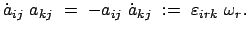 |
(828) |
Überschieben dieser Gleichung mit
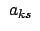 gibt mit den Orthonormierungsrelationen (8.7)
folgenden Ausdruck für die Zeitableitung von
gibt mit den Orthonormierungsrelationen (8.7)
folgenden Ausdruck für die Zeitableitung von 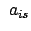 :
:
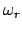 sind die Komponenten des Vektors
sind die Komponenten des Vektors
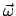 der Winkelgschwindigkeit,
und zwar bezogen auf das raumfeste System
der Winkelgschwindigkeit,
und zwar bezogen auf das raumfeste System 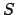 . Diese Komponenten können gemäß Gl. (8.9)
ins bewegte System transformiert werden (
. Diese Komponenten können gemäß Gl. (8.9)
ins bewegte System transformiert werden (
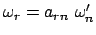 ). Damit,
mit den Orthonormierungsrelationen (8.7) und mit der Transformationsformel für einen
Tensor 3. Stufe
bekommt man aus (8.29a):
). Damit,
mit den Orthonormierungsrelationen (8.7) und mit der Transformationsformel für einen
Tensor 3. Stufe
bekommt man aus (8.29a):
 |
(829a) |
Gln. (8.29a) und (8.29b) dienen zur Ersetzung der
Zeitableitung
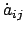 ; Gl. (8.29a) wird
verwendet, wenn man die Winkelgeschwindigkeit im raumfesten System ausdrücken
will, Gl. (8.29a) im körperfesten. In beiden Formeln werden die Größen, die
zunächst in
; Gl. (8.29a) wird
verwendet, wenn man die Winkelgeschwindigkeit im raumfesten System ausdrücken
will, Gl. (8.29a) im körperfesten. In beiden Formeln werden die Größen, die
zunächst in  berechnet worden sind, mittels eines
berechnet worden sind, mittels eines 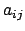 ins körperfeste
System transformiert und umgekehrt.
ins körperfeste
System transformiert und umgekehrt.
Zur Interpretation des Vektors
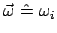 , der in
Gl. (8.28) definiert worden ist, differenzieren wir Gl. (8.5)
(mit
, der in
Gl. (8.28) definiert worden ist, differenzieren wir Gl. (8.5)
(mit
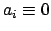 ) nach der Zeit
) nach der Zeit 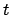 und setzen Gl. (8.5) und
(8.29a) ein:
und setzen Gl. (8.5) und
(8.29a) ein:
Abbildung 8.4:
Vektor der Winkelgeschwindigkeit.
![\includegraphics[scale=0.7]{k8_winkelgeschw}](img1732.gif)
|
Aus dieser Gleichung und aus Abb. 8.4 sieht man, daß der
Vektor
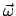 eine Drehung
vermittelt, denn die Geschwindigkeit steht senkrecht zu
eine Drehung
vermittelt, denn die Geschwindigkeit steht senkrecht zu
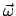 und zu
und zu
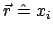 . Der Einheitsvektor
. Der Einheitsvektor
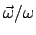 gibt die momentane Drehachse,
der Betrag
gibt die momentane Drehachse,
der Betrag 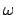 die Geschwindigkeit der Drehung, also die Winkelgeschwindigkeit.
Man kann auch Gl. (8.30) als eine Definition der Winkelgeschwindigkeit betrachten. Man sieht,
daß dieser Vektor nicht eine Ableitung ist, aber über eine Ableitung auf der linken
Seite der Gleichung definiert ist. Deswegen stellt im allg. der Vektor der Winkelgeschwindigkeit
keine Ableitung eines Vektors dar (
die Geschwindigkeit der Drehung, also die Winkelgeschwindigkeit.
Man kann auch Gl. (8.30) als eine Definition der Winkelgeschwindigkeit betrachten. Man sieht,
daß dieser Vektor nicht eine Ableitung ist, aber über eine Ableitung auf der linken
Seite der Gleichung definiert ist. Deswegen stellt im allg. der Vektor der Winkelgeschwindigkeit
keine Ableitung eines Vektors dar (
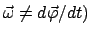 , er ist
anholonom. Solche ''Geschwindigkeiten'', die nur über Linearkombinationen von
Geschwindigkeiten und nicht durch Ableitungen definiert sind, heißen ''Quasikoordinaten''
(vgl. Gl. (11.22)).
Deswegen ist es in manchen Fällen zweckmäßig, von der Winkelgeschwindigkeit auf die
Eulerschen Winkel und deren Zeitableitungen überzugehen. Letztere Größen sind holonom, also
Ableitungen von Funktionen.
, er ist
anholonom. Solche ''Geschwindigkeiten'', die nur über Linearkombinationen von
Geschwindigkeiten und nicht durch Ableitungen definiert sind, heißen ''Quasikoordinaten''
(vgl. Gl. (11.22)).
Deswegen ist es in manchen Fällen zweckmäßig, von der Winkelgeschwindigkeit auf die
Eulerschen Winkel und deren Zeitableitungen überzugehen. Letztere Größen sind holonom, also
Ableitungen von Funktionen.
Die Komponenten der Winkelgeschwindigkeit
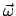 lassen sich auch durch die
Eulerschen Winkel, §8.3, und deren Zeitableitungen ausdrücken.
Dazu wird die gesamte Drehung zerlegt
in eine solche um
lassen sich auch durch die
Eulerschen Winkel, §8.3, und deren Zeitableitungen ausdrücken.
Dazu wird die gesamte Drehung zerlegt
in eine solche um
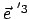 mit der Winkelgeschwindigkeit
mit der Winkelgeschwindigkeit
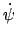 ,
in eine solche um
,
in eine solche um 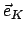 mit der Winkelgeschwindigkeit
mit der Winkelgeschwindigkeit
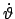 und in die Drehung um
und in die Drehung um
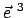 mit der Winkelgeschwindigkeit
mit der Winkelgeschwindigkeit
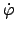 .
Man erhält die Komponenten
.
Man erhält die Komponenten 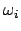 bzw.
bzw. 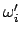 , wenn man für
, wenn man für
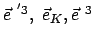 die Komponenten bezüglich
die Komponenten bezüglich 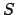 bzw.
bzw.  ,
Gln. (8.16), nimmt.
,
Gln. (8.16), nimmt.
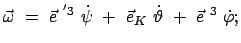 |
(831) |
Die Winkelgeschwindigkeiten
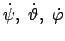 sind Ableitungen der holonomen Koordinaten
sind Ableitungen der holonomen Koordinaten
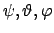 .
Dagegen sind die Komponenten des Vektors der Winkelgeschwindigkeit
.
Dagegen sind die Komponenten des Vektors der Winkelgeschwindigkeit
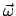 anholonom.
anholonom.
Ableitung der Geschwindigkeit, Beschleunigung und der
Bewegungsgleichungen im bewegten System
Zur Ableitung eines allgemeinen Ausdrucks für die Transformation der
Geschwindigkeit wird Gl. (8.5) nach der Zeit differenziert. Dabei wird
berücksichtigt, daß 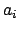 ,
, 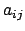 und
und 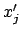 Funktionen der Zeit
sind.
Funktionen der Zeit
sind.
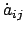 wird mittels Gl. (8.29) eliminiert.
wird mittels Gl. (8.29) eliminiert.
Benutzt man zur Elimination von
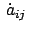 Gl. (8.29b), dann
erhält man eine zweite Gleichung:
Gl. (8.29b), dann
erhält man eine zweite Gleichung:
 |
(832a) |
In der symbolischen Schreibweise der Vektorrechnung wird
Gl. (8.32a) folgendermaßen geschrieben:
 |
(832a) |
Darin bedeutet
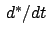 , daß nur die Komponenten von
, daß nur die Komponenten von
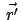 , nicht aber
die zeitlich veränderlichen Basisvektoren von
, nicht aber
die zeitlich veränderlichen Basisvektoren von  nach der Zeit differenziert
werden. Die Schreibweise von Gl. (8.32c) erscheint kompakter als
die der Gln. (8.32a) oder (8.32b). Jedoch besteht in
Gl. (8.32c) manchmal Unklarheit, welche Größen in welchem System zu
berechnen sind. Diese Schwierigkeit wird sehr groß, wenn mehrere Systeme mit
verschiedenen relativen Bewegungen vorkommmen.
nach der Zeit differenziert
werden. Die Schreibweise von Gl. (8.32c) erscheint kompakter als
die der Gln. (8.32a) oder (8.32b). Jedoch besteht in
Gl. (8.32c) manchmal Unklarheit, welche Größen in welchem System zu
berechnen sind. Diese Schwierigkeit wird sehr groß, wenn mehrere Systeme mit
verschiedenen relativen Bewegungen vorkommmen.
Für die zeitliche Änderung eines echten Vektors
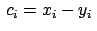 ergibt sich aus
Gl. (8.32a):
ergibt sich aus
Gl. (8.32a):
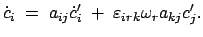 |
(833) |
Speziell für die Winkelgeschwindigkeit
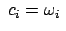 folgt daraus:
folgt daraus:
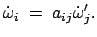 |
(834) |
Differentiation der Gln. (8.32) und nochmalige Verwendung von
Gln. (8.29) gibt für die Beschleunigung
Zur Interpretation der Zentripetalbeschleunigung wählen wir wieder den
Spezialfall von Gl. (8.27) mit
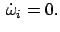
Abbildung 8.5:
Vektor der Zentripetalbeschleunigung.
![\includegraphics[scale=0.7]{k8_zentripetal_beschl}](img1767.gif)
|
Durch die Rotation des Systems wird der Massenpunkt senkrecht zur Drehachse
einwärts beschleunigt (Abb. 8.5). Die Coriolisbeschleunigung erfahren nur
Körper, die sich relativ zu einem rotierenden System bewegen. Das System wird
unter der fliegenden Masse weggedreht. Für einen körperfesten Beobachter ist
die Bahn eines frei fliegenden Körpers nicht mehr eine Gerade.
Die Bewegungsgleichungen im körperfesten System erhält man aus der
im raumfesten Inertialsystem gültigen Bewegungsgleichung
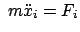 , indem man für
, indem man für
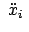 (8.35b) einsetzt und durch
Überschieben mit
(8.35b) einsetzt und durch
Überschieben mit
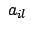 ins körperfeste System
ins körperfeste System  transformiert.
transformiert.
Umordnen der Terme ergibt:
 |
(836) |
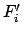 enthält die eingeprägten Kräfte. Wenn diese im raumfesten System
gegeben sind, müssen sie ins körperfeste transformiert werden,
Gl. (8.9). Die anderen Terme auf der rechten Seite von
Gl. (8.36) resultieren aus der Bewegung des Bezugssystems und
werden daher Trägheits- oder Scheinkräfte genannt. Z.B. wird ein im
körperfesten System fixer Punkt bei Rotation zum Zentrum hin
beschleunigt. Ist an diesem Punkt eine Masse, so wird sie sich auf Grund
ihrer Trägheit dieser zentripetalen Beschleunigung widersetzen, sie wird
''scheinbar'' nach außen gezogen (Zentrifugalkraft, vgl. Abb. 8.5.
enthält die eingeprägten Kräfte. Wenn diese im raumfesten System
gegeben sind, müssen sie ins körperfeste transformiert werden,
Gl. (8.9). Die anderen Terme auf der rechten Seite von
Gl. (8.36) resultieren aus der Bewegung des Bezugssystems und
werden daher Trägheits- oder Scheinkräfte genannt. Z.B. wird ein im
körperfesten System fixer Punkt bei Rotation zum Zentrum hin
beschleunigt. Ist an diesem Punkt eine Masse, so wird sie sich auf Grund
ihrer Trägheit dieser zentripetalen Beschleunigung widersetzen, sie wird
''scheinbar'' nach außen gezogen (Zentrifugalkraft, vgl. Abb. 8.5.
Anwendungen
Freier Fall auf der rotierenden Erde
Dieser wird durch Gl. (8.36) beschrieben. Das körperfeste System
 liegt auf der Erdoberfläche (siehe Abb. 8.6).
liegt auf der Erdoberfläche (siehe Abb. 8.6). 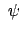 ist die
geographische Breite. Die Transformationsmatrix ist:
ist die
geographische Breite. Die Transformationsmatrix ist:
![$\displaystyle a_{ij}'\;=\;{e'}_i^j\;=\;
\left(\begin{array}{ccc}
\sin\psi \cos\...
...hi & \cos\psi \sin\varphi [0.5em]
-\cos\psi & 0 & \sin\psi
\end{array}\right)$](img1774.gif)
mit
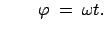
Abbildung 8.6:
Freier Fall auf rotierende Erde.
|
![\includegraphics[scale=0.84]{k8_frei_fall_rot_erde}](img1776.gif) |
Damit ergibt sich für die Komponenten der Winkelgeschwindigkeit:
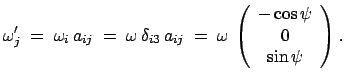 |
(837) |
Dieses Resultat läßt sich auch aus Abb. 8.6 ablesen. Die
Translationsbeschleunigung ist
Die Fallhöhe 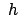 sei klein gegen die Erddimension. Dann kann man mit der
konstanten Fallbeschleunigung
sei klein gegen die Erddimension. Dann kann man mit der
konstanten Fallbeschleunigung 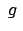 arbeiten. In letzterer ist schon zum
Teil die Führungsbeschleunigung enthalten; diese ist überdies wegen der
Kleinheit der Winkelgeschwindigkeit der Erde
arbeiten. In letzterer ist schon zum
Teil die Führungsbeschleunigung enthalten; diese ist überdies wegen der
Kleinheit der Winkelgeschwindigkeit der Erde
als quadratisch in
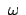 gegenüber der in
gegenüber der in
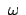 linearen
Coriolisbeschleunigung vernachlässigbar. Damit erhält man aus
(8.36) die Bewegungsgleichung:
linearen
Coriolisbeschleunigung vernachlässigbar. Damit erhält man aus
(8.36) die Bewegungsgleichung:
Dieses System von Differentialgelichungen läßt sich exakt lösen. Doch ist es
zweckmäßiger, ein Näherungsverfahren heranzuziehen. Dieses beruht auf der
Tatsache, daß die Wirkung der Corioliskraft klein ist im Vergleich zur
Fallbeschleunigung. Allgemein wird (8.39) geschrieben als
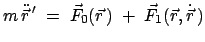 |
(840) |
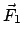 ist hier die Corioliskraft und wegen ihrer Kleinheit im
Vergleich zu
ist hier die Corioliskraft und wegen ihrer Kleinheit im
Vergleich zu
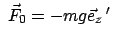 heißt
heißt
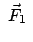 die
Störung. Zuerst wird die ungestörte Bewegungsgleichung
die
Störung. Zuerst wird die ungestörte Bewegungsgleichung
gelöst; man erhält
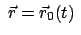 als nullte Näherung. Letztere wird
in die rechte Seite von Gl. (8.40) eingesetzt. Die Gleichung für
die so erhaltene erste Näherung
als nullte Näherung. Letztere wird
in die rechte Seite von Gl. (8.40) eingesetzt. Die Gleichung für
die so erhaltene erste Näherung
 |
(840a) |
läßt sich leichter lösen als die exakte Gl. (8.40). In vielen
Fällen liefert die Lösung von Gl. (8.40b) eine hinreichende
Näherung.
Die Anwendung dieses Verfahrens auf Gl. (8.39) läuft so: Die
Gleichungen der ungestörten Bewegung sind:
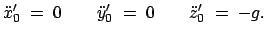 |
(841) |
Ihre Lösungen zu den Anfangsbedingungen sind:
Diese werden in die rechte Seite von Gl. (8.39) eingesetzt und
geben
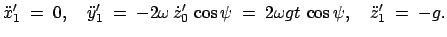 |
(843) |
Integration gibt unter Berücksichtigung der Anfangsbedingungen
(8.42) die folgende erste Näherung:
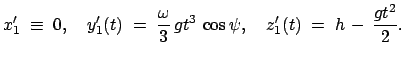 |
(844) |
Die Falldauer 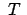 bis zum Boden und die Abweichung in
bis zum Boden und die Abweichung in 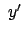 betragen
betragen
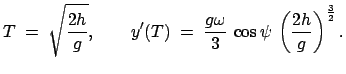 |
(845) |
Für 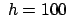 m und
m und
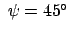 gibt dies eine Ostabweichung
gibt dies eine Ostabweichung
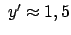 cm.
cm.
Der Foucaultsche Pendelversuch
Der Focaultsche Pendelversuch ist darauf ausgerichtet, die Rotation der Erde
relativ zum Inertialsystem des Fixsternhimmels zu zeigen. Bei der Beobachtung
der Schwingung eines Pendels von einem erdfixen System aus, übt die
Corioliskraft einen Einfluß auf die bewegte Pendelmasse. Wir werden zeigen,
daß sie zu einer Drehung der Schwingungsebene des Pendels relativ zum
Erdsystem führt.
Die Bewegungsgleichung für den Foucaultschen Pendelversuch erhält man aus der
für den freien Fall auf der rotierdenden Erde, Gl. (8.39), indem
man die Nebenbedingung für die Führung auf der Kugelfläche mit dem Radius
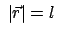 (
( = Pendellänge) hinzufügt:
= Pendellänge) hinzufügt:
Gemäß Gl. (6.6) tritt zu den obigen beiden eingeprägten Kräften in
der Bewegungsgleichung noch die Zwangskraft hinzu. Die neue
Bewegungsgleichung ist daher (mit
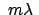 statt mit
statt mit
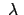 als
Lagrangeschem Multiplikator)
als
Lagrangeschem Multiplikator)
Dieses System wird näherungsweise für kleine Ausschläge gelöst
Wegen der Kleinheit von
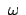 , Gl. (8.38), wird in der
letzten der obigen Bewegungsgleichungen (8.47) der Term
proportional
, Gl. (8.38), wird in der
letzten der obigen Bewegungsgleichungen (8.47) der Term
proportional
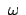 gegen
gegen 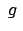 vernachlässigt. Für kleine Ausschläge
gestattet die resultierende Gleichung den Lagrangeschen Multiplikator zu
bestimmen:
vernachlässigt. Für kleine Ausschläge
gestattet die resultierende Gleichung den Lagrangeschen Multiplikator zu
bestimmen:
Dieser Wert wird in die beiden Bewegungsgleichungen für  und
und 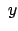 ,
Gl. (8.47), eingesetzt; die resultierenden Gleichungen werden zu
einer einzigen Differentialgleichung für die komplexe Variable
,
Gl. (8.47), eingesetzt; die resultierenden Gleichungen werden zu
einer einzigen Differentialgleichung für die komplexe Variable 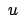 vereinigt:
vereinigt:
Letztere wird durch Exponentialansatz gelöst
Zu den Anfangsbedingungen
ergibt sich als Lösung und deren Zeitableitung:
Da
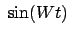 Nullstellen hat, verschwindet
Nullstellen hat, verschwindet 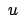 für diese Werte von
für diese Werte von
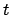 ; es sind also
; es sind also
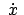 und
und
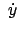 gleichzeitig Null, die
Bahnkurve hat an diesen Stellen Spitzen; s. Abb. 8.7. Die Zeit zwischen dem
Durchlaufen zweier aufeinanderfolgender Spitzen, also der Abstand zweier
aufeinanderfolgender Nullstellen von
gleichzeitig Null, die
Bahnkurve hat an diesen Stellen Spitzen; s. Abb. 8.7. Die Zeit zwischen dem
Durchlaufen zweier aufeinanderfolgender Spitzen, also der Abstand zweier
aufeinanderfolgender Nullstellen von
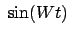 , ist die halbe
Schwingungsdauer
, ist die halbe
Schwingungsdauer 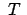 des Pendels
Der Winkel
des Pendels
Der Winkel
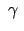 zwischen den momentanen Schwingungsebenen zur Zeit
zwischen den momentanen Schwingungsebenen zur Zeit
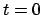 und zur Zeit
und zur Zeit 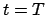 ist
ist
Zum Abschluß ein Zahlenbeispiel für
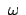 aus (8.38):
aus (8.38):
Abbildung 8.7:
Drehung der Schwingungsebenen eines Pendels aufgrund der Rotation
der Erde. Die Breitenabhängigkeit des Foucaultschen Pendels wird im
Notebook K8FoucaultP.nb
simuliert.
![\includegraphics[scale=0.7]{k8_focault}](img1873.gif)
|
Die Lamorpräzession
In einem Inertialsystem werde einem gegebenen eingeprägten Kraftfeld
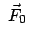 ein homogenes Magnetfeld
ein homogenes Magnetfeld
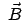 überlagert, das so
schwach ist, daß die Lorentzkraft auf ein Teilchen der Ladung
überlagert, das so
schwach ist, daß die Lorentzkraft auf ein Teilchen der Ladung 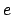 klein ist
im Vergleich zu
klein ist
im Vergleich zu
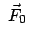 . Das Theorem von Larmor besagt, daß
unter dieser Bedingung die Lorentzkraft nur zu einer Rotation der ungestörten
Bahn mit der Winkelgeschwindigkeit
. Das Theorem von Larmor besagt, daß
unter dieser Bedingung die Lorentzkraft nur zu einer Rotation der ungestörten
Bahn mit der Winkelgeschwindigkeit
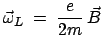 |
(852) |
(Larmorpräzession) führt.
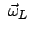 heißt Lamorfrequenz. Z.B. ein
Elektron bewegt sich im elektorstatischen Feld des Atomkerns. Seine Bahn ist
eine Keplerellipse. Wird dieses Atom in ein schaches homogenes Magnetfeld
gebracht, dann rotiert die Keplerellipse mit
heißt Lamorfrequenz. Z.B. ein
Elektron bewegt sich im elektorstatischen Feld des Atomkerns. Seine Bahn ist
eine Keplerellipse. Wird dieses Atom in ein schaches homogenes Magnetfeld
gebracht, dann rotiert die Keplerellipse mit
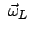 um die
magnetische Feldrichtung. In einem beliebigen Zentralkraftfeld ist die Bahn
eben. Unter dem Einfluß des zusätzlichen schwachen Magnetfeldes rotiert die
Bahnnormale (prop. dem Drehimpulsvektor) mit der Frequenz
um die
magnetische Feldrichtung. In einem beliebigen Zentralkraftfeld ist die Bahn
eben. Unter dem Einfluß des zusätzlichen schwachen Magnetfeldes rotiert die
Bahnnormale (prop. dem Drehimpulsvektor) mit der Frequenz
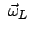 auf einem Kegel, dessen Achse mit der Richtung des
Magnetfeldes zusammenfällt.
auf einem Kegel, dessen Achse mit der Richtung des
Magnetfeldes zusammenfällt.
Dieses Theorem ist besonders wichtig in der Atomphysik für Systeme mit
mehreren Elektronen; deren Bewegungsgleichungen lassen sich nur schwer
lösen. Das Larmorsche Theorem gestattet es, die Aufspaltung der
Spektrallinien durch ein Magnetfeld, den ZEEMANEFFEKT, unmittelbar
zu berechnen.
Zur Illustration betrachten wir einen harmonischen Oszillator in einem
Magnetfeld. Der Einfachheit halber nehmen wir an, die Anfangsbedingungen
seien derart, daß die Bewegung auf die Ebene senkrecht zu
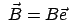 (
(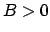 ) beschränkt ist
Die beiden Bewegungsgleichungen werden, wie angedeutet, zu einer komplexen
vereinigt und diese mittels Exponentialansatz gelöst
) beschränkt ist
Die beiden Bewegungsgleichungen werden, wie angedeutet, zu einer komplexen
vereinigt und diese mittels Exponentialansatz gelöst
Bei der Berechung der Näherungswerte für
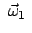 und
und
 wurde berücksichtigt, daß die Lorentzkraft klein ist
gegnüber der elastischen Bindung, d.h.
wurde berücksichtigt, daß die Lorentzkraft klein ist
gegnüber der elastischen Bindung, d.h.
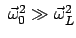 . Man sieht bereits hier, daß in dieser Näherung die
Bewegung im Magnetfeld beschrieben ist durch den Ausdruck in der Klammer, der
einer ungestörten Oszillation entspricht, während der Vorfaktor die Rotation
mit der Larmorfrequenz
. Man sieht bereits hier, daß in dieser Näherung die
Bewegung im Magnetfeld beschrieben ist durch den Ausdruck in der Klammer, der
einer ungestörten Oszillation entspricht, während der Vorfaktor die Rotation
mit der Larmorfrequenz
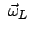 widergibt. Setzen wir
widergibt. Setzen wir
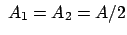 ,
, 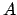 reell, so entspricht dies einer Oszillation längs des
Strahls
reell, so entspricht dies einer Oszillation längs des
Strahls
![$ \;x'\in[-A, A]$](img1890.gif) ,
, 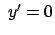 ; die vollständige Näherungslösung enthält
zusätzlich eine Rotation dieser Strecke mit der Larmorfrequenz
; die vollständige Näherungslösung enthält
zusätzlich eine Rotation dieser Strecke mit der Larmorfrequenz
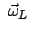 .
.
Beweis des Larmorschen Theorems: In einem Inertialsystem lautet die
Bewegungsgleichung:
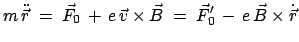 |
(853) |
In einem System, das mit konstanter Winkelgeschwindigkeit
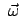 rotiert, lautet die Bewegungsgleichung (Gl. (8.53))
rotiert, lautet die Bewegungsgleichung (Gl. (8.53))
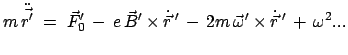 |
(854) |
Der Zentrifugalterm kann vernachläßigt werden, wenn
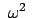 klein ist. Dann heben sich die Lorentzkraft und die Corioliskraft auf, wenn
klein ist. Dann heben sich die Lorentzkraft und die Corioliskraft auf, wenn
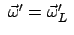 gewählt wird. Wegen Gl. (8.9)
gilt dann die Behauptung (8.52).
gewählt wird. Wegen Gl. (8.9)
gilt dann die Behauptung (8.52).
Ist
 eine Zentralkraft, dann ist der Drehimpuls zeitlich
konstant in einem Inertialsystem. Für
eine Zentralkraft, dann ist der Drehimpuls zeitlich
konstant in einem Inertialsystem. Für
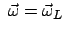 und
unter den angegebenen Näherungen hat auch die Bewegungsgleichung
(8.54) die gleiche Form wie in einem Inertialsystem. Im
rotierenden System ist also der Drehimpulsvektor zeitlich konstant. Gemäß
(8.9) und (8.33) gilt dann im raumfesten System:
und
unter den angegebenen Näherungen hat auch die Bewegungsgleichung
(8.54) die gleiche Form wie in einem Inertialsystem. Im
rotierenden System ist also der Drehimpulsvektor zeitlich konstant. Gemäß
(8.9) und (8.33) gilt dann im raumfesten System:
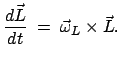 |
(855) |
Es ist nicht schwer mit Hilfe dieser Gleichung zu zeigen, daß das Quadrat
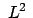 und die Komponente von
und die Komponente von
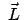 in Richtung von
in Richtung von
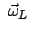 , also
, also  , konstant sind. Der Drehimpulsvektor
bewegt sich also auf einem Kegel, dessen Achse mit der Feldrichtung
zusammenfällt.
, konstant sind. Der Drehimpulsvektor
bewegt sich also auf einem Kegel, dessen Achse mit der Feldrichtung
zusammenfällt.
Mitbewegte Basissysteme für krummlinige orthogonale
Koordinatensystem
Die Problemstellung wird zuerst an einem Beispiel erklärt. Die Bewegung eines
Massenpunktes soll in ebenen Polarkoordinaten beschrieben werden
(Abb. 8.8). Der Ortsvektor
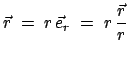 |
(856) |
Abbildung 8.8:
Bewegung eines Massenpunktes.
|
![\includegraphics[scale=0.75]{k8_krumml_koord}](img1904.gif) |
der die augenblickliche Lage des Massenpunktes angibt, läuft mit dem bewegten
Massenpunkt mit; damit dreht sich
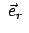 mit der Bewegung des
Massenpunktes mit.
mit der Bewegung des
Massenpunktes mit. 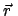 und
und
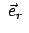 sind beide Funktionen der
Zeit. Ebenso dreht sich der zu
sind beide Funktionen der
Zeit. Ebenso dreht sich der zu
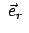 senkrechte Einheitsvektor
senkrechte Einheitsvektor
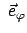 . Dies muß bei der Berechnung der Geschwindigkeit und
der Beschleunigung berücksichtigt werden. Im Zeitintervall
. Dies muß bei der Berechnung der Geschwindigkeit und
der Beschleunigung berücksichtigt werden. Im Zeitintervall 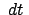 bewegt
sich der Massenpunkt P nach P'. Aus Abb. 8.8
ersieht man, daß die Inkremente
bewegt
sich der Massenpunkt P nach P'. Aus Abb. 8.8
ersieht man, daß die Inkremente
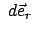 und
und
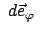 gegeben sind durch
gegeben sind durch
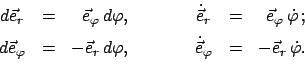 |
(857) |
Diese Transformationsgleichungen erhält man auch auf folgende Weise. Man gibt
die Einheitsvektoren
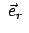 und
und
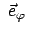 in
kartesischen Koordinaten an:
in
kartesischen Koordinaten an:
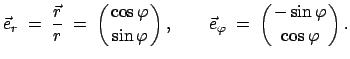 |
(858) |
Differentiation nach der Zeit gibt dann wieder
Dieses Verfahren ist bei komplizierten krummlinigen Koordinatensystemen
leichter durchzuführen als die der Abb. 8.8
entsprechenden geometrischen Überlegungen.
Mit Hilfe der Gln. (8.57) erhält man für die Geschwindigkeit und
Beschleunigung:
Für die Bewegung eines Massenpunktes im Felde einer Zentralkraft ergibt sich,
wenn man ebene Polarkoordinaten in der Bahnebene mit dem Ursprung im
Kraftzentrum ( ) verwendet:
) verwendet:
In Zylinderkoordinaten 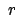 ,
, 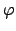 ,
, 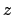 findet man mittels
Gln. (8.57) an Stelle von Gln. (8.56) und
(8.59)
findet man mittels
Gln. (8.57) an Stelle von Gln. (8.56) und
(8.59)
Das in Gln. (8.58) und (8.57a) verwendete Verfahren wird
nun allgemein für beliebige krummlinige orthogonale Koordinaten 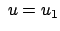 ,
,
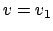 ,
, 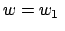 angeschrieben. Aus geometrischen Überlegungen berechnet
man die Einheitsvektoren
angeschrieben. Aus geometrischen Überlegungen berechnet
man die Einheitsvektoren
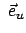 ,
, 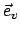 ,
,
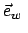 in
kartesischen Koordinaten. Dies sind die normierten Tangentenvektoren an die
drei Raumkurven
in
kartesischen Koordinaten. Dies sind die normierten Tangentenvektoren an die
drei Raumkurven
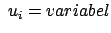 ,
,
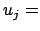 const.,
const.,
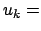 const.
const.
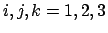 und zyklisch.
und zyklisch.
Daraus findet man die Zeitableitung der Vektoren
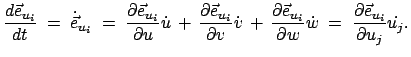 |
(863) |
Die drei partiellen Ableitungen jedes Einheitsvektors lassen sich auf das
vollständige System von Basisvektoren aufspannen:
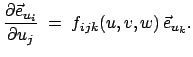 |
(864) |
Die 27 Funktionen
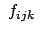 hängen von den
hängen von den 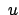 ,
, 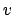 ,
, 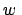 ab. Einsetzen von Gl. (8.64) in Gl. (8.63) gibt:
ab. Einsetzen von Gl. (8.64) in Gl. (8.63) gibt:
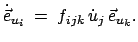 |
(865) |
Aus der Orthogonalität der Basisvektoren
(
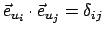 ) und ihrer Normiertheit
(
) und ihrer Normiertheit
(
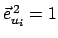 ,
,
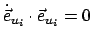 ) folgt:
) folgt:
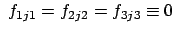 . Der Ortsvektor
. Der Ortsvektor
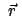 wird auf
die Basisvektoren aufgespannt:
wird auf
die Basisvektoren aufgespannt:
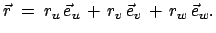 |
(866) |
Zur Berechnung der Geschwindigkeit werden die Zeitableitungen der
Einheitsvektoren durch die Ausdrücke von Gl. (8.65) ersetzt:
Differentiation von
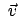 und nochmalige Anwendung von
Gl. (8.65) gibt die entsprechenden Ausdrücke für die Komponenten
der Beschleunigung.
und nochmalige Anwendung von
Gl. (8.65) gibt die entsprechenden Ausdrücke für die Komponenten
der Beschleunigung.
Z.B. lauten in Kugelkoordinaten 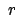 ,
, 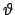 ,
, 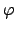 die
Basiseinheitsvektoren:
die
Basiseinheitsvektoren:
Den Gleichungen (8.65) (vgl. (8.57)) entsprechen nun:
Damit erhält man für Lage, Geschwindigkeit und Beschleunigung:
Damit erhält man für die Bewegungsgleichung im Felde einer Zentralkraft:
Die in der letzten Zeile benützte Komponente des Drehimpulses findet man aus:
Das Quadrat des Drehimpulses setzt man in die erste der obigen
Bewegungsgleichungen (8.68) ein, ebenso das Potential für die
radiale Kraft
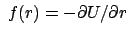 . Dann erhält man den
Energiesatz:
. Dann erhält man den
Energiesatz:
![$\displaystyle \frac{dE}{dt}\;=\;\frac{d}{dt}\left[\frac{m}{2}\left(\dot{r}^2 + \frac{L^2}{m^2r^2} \right) + U(r) \right] \;=\;0.$](img1978.gif) |
(870) |
Christian Sommer
2003-01-27
![\includegraphics[scale=0.8]{k8_vec_drehung}](img1615.gif) []
[]
![\includegraphics[scale=0.84]{k8_koordsys_drehung}](img1616.gif)
![]() gegenüber dem ungestrichenen
gegenüber dem ungestrichenen ![]() um den Winkel
um den Winkel ![]() verdreht
ist, ergibt sich (Abb. 8.2(b)):
verdreht
ist, ergibt sich (Abb. 8.2(b)):
![]() schiebt man den einen Ursprung in den anderen; 2) durch eine Drehung bringt man entsprechende
Koordinatenachsen zur Deckung. Diese Drehung kann auf mehrere Weisen festgelegt werden. Hier
werden nur zwei behandelt: a) die Angabe eines Drehvektors: b) durch drei Winkel, die
Eulerschen Winkel.
schiebt man den einen Ursprung in den anderen; 2) durch eine Drehung bringt man entsprechende
Koordinatenachsen zur Deckung. Diese Drehung kann auf mehrere Weisen festgelegt werden. Hier
werden nur zwei behandelt: a) die Angabe eines Drehvektors: b) durch drei Winkel, die
Eulerschen Winkel.
![]() in Gl. (8.5) Null.
Eine Drehung kann durch die Angabe eines Einheitsvektors
in Gl. (8.5) Null.
Eine Drehung kann durch die Angabe eines Einheitsvektors ![]() für die Drehachse und
eines Drehwinkels
für die Drehachse und
eines Drehwinkels ![]() festgelegt werden. Dann kann man die Komponenten der Basisvektoren
des gedrehten Systems
festgelegt werden. Dann kann man die Komponenten der Basisvektoren
des gedrehten Systems ![]() mittels des Drehtensors berechnen:
mittels des Drehtensors berechnen:
![]() relativ zu raumfesten
relativ zu raumfesten ![]() an. Letzteres wird in seine in Abb. 8.3
angegebene Endlage in 3 Schritten übergeführt:
Zuerst wird das gestrichene System um die 3-Achse (die 3'-Achse fällt während dieses
Schrittes noch mit der 3-Achse zusammen) um den Winkel
an. Letzteres wird in seine in Abb. 8.3
angegebene Endlage in 3 Schritten übergeführt:
Zuerst wird das gestrichene System um die 3-Achse (die 3'-Achse fällt während dieses
Schrittes noch mit der 3-Achse zusammen) um den Winkel ![]() in positivem Sinn gedreht.
Die neue Lage der 1'-Achse heißt die Knotenlinie.
Im zweiten Schritt wird das körperfeste System um die Knotenlinie um
den Winkel
in positivem Sinn gedreht.
Die neue Lage der 1'-Achse heißt die Knotenlinie.
Im zweiten Schritt wird das körperfeste System um die Knotenlinie um
den Winkel ![]() gedreht. Diesen Winkel schließen auch die 1'-, 2'-Ebene
und die 1-, 2-Ebene ein. Die momentane Stellung der 2'-Achse gibt die
Querachse. Im letzten Schritt werden die 1'- und 2'-Achse um den Winkel
gedreht. Diesen Winkel schließen auch die 1'-, 2'-Ebene
und die 1-, 2-Ebene ein. Die momentane Stellung der 2'-Achse gibt die
Querachse. Im letzten Schritt werden die 1'- und 2'-Achse um den Winkel
![]() um die 3'-Achse in die Endlage gedreht.
um die 3'-Achse in die Endlage gedreht.
![]() beider Systeme zum Punkt
beider Systeme zum Punkt ![]() weisende Vektor
weisende Vektor ![]() hat in
hat in ![]() die Komponenten
die Komponenten ![]() , in
, in ![]() die Komponenten
die Komponenten ![]() .
.
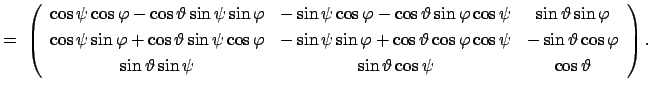
![$\displaystyle A(\vec{e}^{ 1}, \vartheta) = \
\left( \begin{array}{ccc}
1 &...
...n \vartheta [1mm]
0 & \sin \vartheta & \cos \vartheta \end{array} \right) .
$](img1656.gif)
![]() überschoben, der resultierende
Ausdruck wird mit Gl. (8.5) verglichen. Dies gibt:
überschoben, der resultierende
Ausdruck wird mit Gl. (8.5) verglichen. Dies gibt:
![]() ändert sich im
Laufe der Zeit. In
der Transformationsgleichung (8.5) sind der Vektor
ändert sich im
Laufe der Zeit. In
der Transformationsgleichung (8.5) sind der Vektor
![]() und die Matrixelemente
und die Matrixelemente
![]() Funktionen der Zeit. Dies muß bei der Berechnung der Geschwindigkeit
Funktionen der Zeit. Dies muß bei der Berechnung der Geschwindigkeit
![]() und der Beschleunigung
und der Beschleunigung
![]() berücksichtigt werden.
berücksichtigt werden.
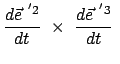
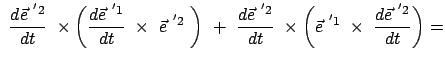
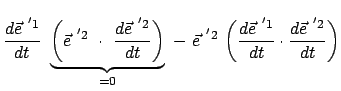
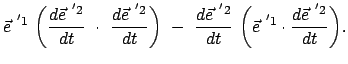
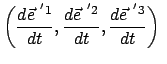
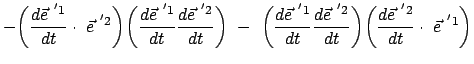
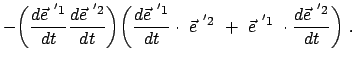
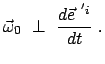
![]() ist der Vektor der Winkelgeschwindigkeit, wie er auch unten
in Gl. (8.28) definiert ist. Seine Richtung gibt die Richtung der Drehachse, seine Länge
den Betrag der Winkelgeschwindigkeit an.
ist der Vektor der Winkelgeschwindigkeit, wie er auch unten
in Gl. (8.28) definiert ist. Seine Richtung gibt die Richtung der Drehachse, seine Länge
den Betrag der Winkelgeschwindigkeit an.
![]() gemäß
Gl. (8.22) ersetzt.
Dies gibt dann:
gemäß
Gl. (8.22) ersetzt.
Dies gibt dann:
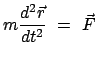
![]() des
Translationsvektors
und die Elemente
des
Translationsvektors
und die Elemente ![]() der Drehmatrix gegebene Funktionen der Zeit. Wieder ist eine
gesonderte Untersuchung der Zeitableitung dieser Matrix nötig; dies führt
neuerlich auf den
Vektor der Winkelgeschwindigkeit mit den Komponenten
der Drehmatrix gegebene Funktionen der Zeit. Wieder ist eine
gesonderte Untersuchung der Zeitableitung dieser Matrix nötig; dies führt
neuerlich auf den
Vektor der Winkelgeschwindigkeit mit den Komponenten ![]() .
.
![]() ; daher
ist
; daher
ist ![]() . Ebenso sei der Punkt
. Ebenso sei der Punkt ![]() fix in
fix in ![]() (Abb. 8.3):
(Abb. 8.3):
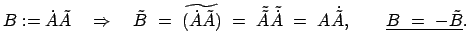
![]() , der in
Gl. (8.28) definiert worden ist, differenzieren wir Gl. (8.5)
(mit
, der in
Gl. (8.28) definiert worden ist, differenzieren wir Gl. (8.5)
(mit
![]() ) nach der Zeit
) nach der Zeit ![]() und setzen Gl. (8.5) und
(8.29a) ein:
und setzen Gl. (8.5) und
(8.29a) ein:
![]() eine Drehung
vermittelt, denn die Geschwindigkeit steht senkrecht zu
eine Drehung
vermittelt, denn die Geschwindigkeit steht senkrecht zu
![]() und zu
und zu
![]() . Der Einheitsvektor
. Der Einheitsvektor
![]() gibt die momentane Drehachse,
der Betrag
gibt die momentane Drehachse,
der Betrag ![]() die Geschwindigkeit der Drehung, also die Winkelgeschwindigkeit.
Man kann auch Gl. (8.30) als eine Definition der Winkelgeschwindigkeit betrachten. Man sieht,
daß dieser Vektor nicht eine Ableitung ist, aber über eine Ableitung auf der linken
Seite der Gleichung definiert ist. Deswegen stellt im allg. der Vektor der Winkelgeschwindigkeit
keine Ableitung eines Vektors dar (
die Geschwindigkeit der Drehung, also die Winkelgeschwindigkeit.
Man kann auch Gl. (8.30) als eine Definition der Winkelgeschwindigkeit betrachten. Man sieht,
daß dieser Vektor nicht eine Ableitung ist, aber über eine Ableitung auf der linken
Seite der Gleichung definiert ist. Deswegen stellt im allg. der Vektor der Winkelgeschwindigkeit
keine Ableitung eines Vektors dar (
![]() , er ist
anholonom. Solche ''Geschwindigkeiten'', die nur über Linearkombinationen von
Geschwindigkeiten und nicht durch Ableitungen definiert sind, heißen ''Quasikoordinaten''
(vgl. Gl. (11.22)).
Deswegen ist es in manchen Fällen zweckmäßig, von der Winkelgeschwindigkeit auf die
Eulerschen Winkel und deren Zeitableitungen überzugehen. Letztere Größen sind holonom, also
Ableitungen von Funktionen.
, er ist
anholonom. Solche ''Geschwindigkeiten'', die nur über Linearkombinationen von
Geschwindigkeiten und nicht durch Ableitungen definiert sind, heißen ''Quasikoordinaten''
(vgl. Gl. (11.22)).
Deswegen ist es in manchen Fällen zweckmäßig, von der Winkelgeschwindigkeit auf die
Eulerschen Winkel und deren Zeitableitungen überzugehen. Letztere Größen sind holonom, also
Ableitungen von Funktionen.
![]() lassen sich auch durch die
Eulerschen Winkel, §8.3, und deren Zeitableitungen ausdrücken.
Dazu wird die gesamte Drehung zerlegt
in eine solche um
lassen sich auch durch die
Eulerschen Winkel, §8.3, und deren Zeitableitungen ausdrücken.
Dazu wird die gesamte Drehung zerlegt
in eine solche um
![]() mit der Winkelgeschwindigkeit
mit der Winkelgeschwindigkeit
![]() ,
in eine solche um
,
in eine solche um ![]() mit der Winkelgeschwindigkeit
mit der Winkelgeschwindigkeit
![]() und in die Drehung um
und in die Drehung um
![]() mit der Winkelgeschwindigkeit
mit der Winkelgeschwindigkeit
![]() .
Man erhält die Komponenten
.
Man erhält die Komponenten ![]() bzw.
bzw. ![]() , wenn man für
, wenn man für
![]() die Komponenten bezüglich
die Komponenten bezüglich ![]() bzw.
bzw. ![]() ,
Gln. (8.16), nimmt.
,
Gln. (8.16), nimmt.
![]() ,
, ![]() und
und ![]() Funktionen der Zeit
sind.
Funktionen der Zeit
sind.
![]() wird mittels Gl. (8.29) eliminiert.
wird mittels Gl. (8.29) eliminiert.
![$\displaystyle =\;\omega^2\left[\frac{\vec{\omega}}{\omega} \left(\frac{\vec{\om...
...omega}\cdot\vec{r} \right)\;-\;\vec{r} \right]\;=\; -\omega^2 \vec{r}_{\perp}$](img1766.gif)
![]() , indem man für
, indem man für
![]() (8.35b) einsetzt und durch
Überschieben mit
(8.35b) einsetzt und durch
Überschieben mit
![]() ins körperfeste System
ins körperfeste System ![]() transformiert.
transformiert.
![]() enthält die eingeprägten Kräfte. Wenn diese im raumfesten System
gegeben sind, müssen sie ins körperfeste transformiert werden,
Gl. (8.9). Die anderen Terme auf der rechten Seite von
Gl. (8.36) resultieren aus der Bewegung des Bezugssystems und
werden daher Trägheits- oder Scheinkräfte genannt. Z.B. wird ein im
körperfesten System fixer Punkt bei Rotation zum Zentrum hin
beschleunigt. Ist an diesem Punkt eine Masse, so wird sie sich auf Grund
ihrer Trägheit dieser zentripetalen Beschleunigung widersetzen, sie wird
''scheinbar'' nach außen gezogen (Zentrifugalkraft, vgl. Abb. 8.5.
enthält die eingeprägten Kräfte. Wenn diese im raumfesten System
gegeben sind, müssen sie ins körperfeste transformiert werden,
Gl. (8.9). Die anderen Terme auf der rechten Seite von
Gl. (8.36) resultieren aus der Bewegung des Bezugssystems und
werden daher Trägheits- oder Scheinkräfte genannt. Z.B. wird ein im
körperfesten System fixer Punkt bei Rotation zum Zentrum hin
beschleunigt. Ist an diesem Punkt eine Masse, so wird sie sich auf Grund
ihrer Trägheit dieser zentripetalen Beschleunigung widersetzen, sie wird
''scheinbar'' nach außen gezogen (Zentrifugalkraft, vgl. Abb. 8.5.
![]() liegt auf der Erdoberfläche (siehe Abb. 8.6).
liegt auf der Erdoberfläche (siehe Abb. 8.6). ![]() ist die
geographische Breite. Die Transformationsmatrix ist:
ist die
geographische Breite. Die Transformationsmatrix ist:
![$\displaystyle a_{ij}'\;=\;{e'}_i^j\;=\;
\left(\begin{array}{ccc}
\sin\psi \cos\...
...hi & \cos\psi \sin\varphi [0.5em]
-\cos\psi & 0 & \sin\psi
\end{array}\right)$](img1774.gif) mit
mit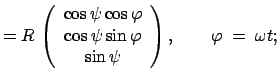
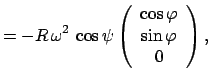
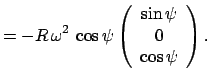
![]() (
(![]() = Pendellänge) hinzufügt:
= Pendellänge) hinzufügt:
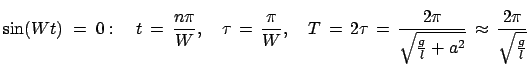
![\includegraphics[scale=0.7]{k8_focault}](img1873.gif)
![]() ein homogenes Magnetfeld
ein homogenes Magnetfeld
![]() überlagert, das so
schwach ist, daß die Lorentzkraft auf ein Teilchen der Ladung
überlagert, das so
schwach ist, daß die Lorentzkraft auf ein Teilchen der Ladung ![]() klein ist
im Vergleich zu
klein ist
im Vergleich zu
![]() . Das Theorem von Larmor besagt, daß
unter dieser Bedingung die Lorentzkraft nur zu einer Rotation der ungestörten
Bahn mit der Winkelgeschwindigkeit
. Das Theorem von Larmor besagt, daß
unter dieser Bedingung die Lorentzkraft nur zu einer Rotation der ungestörten
Bahn mit der Winkelgeschwindigkeit